Les risques : comment les mathématiques aident à les évaluer

Après les phases de perception et d'identification des risques, dans laquelle le facteur humain et culturel joue un rôle essentiel, on doit aussi évaluer les risques en tenant compte des conséquences possibles...

Dans cette phase d'évaluation, on prend maintenant en compte l'ensemble des paramètres de la vulnérabilité : causes (facteurs de risques ou périls), objets de risque (les organisations ou ressources à risque), et conséquences avec leurs gravités potentielles.

L’approche statistique
De même que les mathématiciens ont voulu quantifier le hasard en inventant les probabilités, les économistes ont voulu quantifier l'incertitude économique en modélisant les risques. Cette quantification qui garde toujours un côté plus ou moins estimatif, est réalisée à partir de séries statistiques historiques. La théorie financière tend à confondre le risque réel d'un actif financier et l'indicateur de risque qu'est la volatilité passée du prix de cet actif, bien que rien ne dise que les évolutions passées soient un bon indicateur du futur.

Les probabilités subjectives ou objectives, des algorithmes de calcul dont la célèbre méthode de Monte-Carlo ou des scénarios futurs de gains et pertes, peuvent également être mis en jeu. C'est ainsi que, la théorie financière a fortement développé l'utilisation de mathématiques probabilistes pour estimer la valeur des actifs. En principe, plus le risque pesant sur un actif est fort, plus son prix sur le marché est bas et son rendement attendu élevé, si du moins le marché est efficient. Cette approche est surtout adoptée dans les milieux ou l'on peut disposer de statistiques et de modèles pour les exploiter. C'est en particulier le cas pour les milieux financiers. C'est pourquoi les experts en gestion des risques ont développé une méthode d'évaluation appelée "fréquence - gravité" qui consiste à calculer un poids du risque à partir de plusieurs critères.

Les différents critères (généralement évalués de 1 à 4) varient selon experts et méthodes, mais on retrouve généralement la fréquence du risque quantifiant la probabilité que le risque devienne réalité, la gravité de la conséquence et la maîtrise par les personnes concernées des risques dans le domaine. Ces critères sont évalués, parfois de manière subjective. Ils sont ensuite multipliés, donnant un chiffre (donc de 1 à 64) permettant de classifier et attribuer une priorité de traitement du risque. Selon la définition scientifique du risque (D. Bernoulli), l'approche subjective, par la méthode "fréquence-gravité" qui nous autorise à estimer d'une part, des "plausibilités" ou des "vraisemblances" selon le terme de Marcel Boll (mathématicien français) et d'autre part, des conséquences, conduit à la valeur d'un aléa (c'est-à-dire d'un événement dangereux prédéterminé) et non à un risque (le risque possédant une notion plus globale ; voir "Définition scientifique du risque").

Aussi, pour estimer un risque (sans historique statistique) il faut prédéterminer plusieurs événements possibles de même nature, estimer leurs plausibilités (leur somme devant être égale à 1 - la somme des probabilités étant égale à 1) estimer leurs conséquences possibles puis estimer chaque aléa. La réelle valeur scientifique du risque sera alors la somme des aléas.

Définition scientifique du risque
Daniel Bernoulli, en 1738, apporte la première définition scientifique : « le risque est l'espérance mathématique d'une fonction de probabilité d'événements ». En termes plus simples, il s'agit de la valeur moyenne des conséquences d'événements affectés de leur probabilité. Ainsi, un événement e1 a une probabilité d'occurrence p1 avec une conséquence probable C1 ; de même un événement en aura une probabilité pn et une conséquence Cn, alors le risque r vaudra

r = p1⋅C1 + p2⋅C2 + … + pn⋅Cn = ∑pi⋅Ci

Le produit pi⋅Ci est appelé valeur de l'aléa i.

Cette définition implique, pour le calcul du risque, la connaissance d'une suite statistique d'événements ou pour le moins une estimation approchée ou subjective des diverses plausibilités (probabilités supposées) et des conséquences des aléas imaginés, lorsque l'on ne dispose par d'historiques d'événements et que malgré cela on souhaite évaluer un risque. Si l'on a fait une analyse exhaustive, alors, toutes les situations ayant été identifiées, on a ∑pi = 1 et donc :

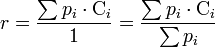
Le risque est donc le barycentre des événements, ou, pour prendre une métaphore tirée de la physique, il apparaît comme le centre de gravité des conséquences des événements pondérés par les probabilités d'occurrence. On notera avec intérêt que le risque est la somme des aléas et que le produit de la fréquence et de la gravité souvent évoqué ne représente nullement le risque mais seulement la valeur d'un aléa déterminé.

La difficulté est souvent de chiffrer les probabilités pi et les conséquences Ci. Cela est simple dans certains cas, comme par exemple pour les jeux de loterie, il est en revanche plus compliqué de chiffrer la probabilité d'occurrence d'événements rares ou d'événements probables mais n'ayant jamais eu lieu (domaine innovant), et de chiffrer les conséquences en général : quel chiffre mettre derrière une blessure, un décès, une atteinte morale, une pollution de l'environnement ?

Un actuaire, spécialiste des calculs de risques :

75015 - AJMB ACTUAIRES http://www.passif-social.fr